Résumé
Aux premières heures du 4 novembre 2020, le candidat démocrate Joe Biden a reçu plusieurs “pics de voix” importants qui ont amélioré de manière substantielle – et décisive – sa position électorale dans le Michigan, le Wisconsin et la Géorgie. Ces “pics de voix” suscitent beaucoup de scepticisme et d’incertitude. Les critiques mettent en avant des pratiques de comptage de voix suspectes, des différences extrêmes entre les décomptes de voix des deux principaux candidats et le moment où les mises à jour des votes ont été effectuées, entre autres facteurs, pour mettre en doute la légitimité de certains de ces pics. Si l’analyse des données ne peut à elle seule démontrer l’existence d’une fraude ou de problèmes systémiques, elle peut nous indiquer des cas statistiquement anormaux qui méritent un examen plus approfondi.
C’est l’un de ces cas : Notre analyse révèle que quelques mises à jour de votes clés dans des États compétitifs étaient inhabituellement importantes et présentaient un ratio Biden/Trump anormalement élevé. Nous démontrons que les résultats diffèrent suffisamment des résultats attendus pour être une source de préoccupation.
Dans ce rapport, nous nous appuyons uniquement sur les données publiques du New York Times pour identifier et analyser les anomalies statistiques dans les États clés. En examinant 8 954 mises à jour individuelles des votes (différences dans les totaux des votes pour chaque candidat entre les changements successifs des totaux des votes courants, appelés familièrement “dumps” ou “lots”), nous découvrons une propriété mathématique remarquablement cohérente : il existe une relation inverse claire entre la différence dans les totaux des votes des candidats et le rapport des totaux des votes. (En d’autres termes, il n’est pas surprenant de voir des mises à jour de votes avec des marges importantes, et il n’est pas surprenant de voir des mises à jour de votes avec des ratios de soutien très importants entre les candidats, mais il est surprenant de voir des mises à jour de votes qui sont les deux).
L’importance de cette propriété sera expliquée plus en détail dans les sections ultérieures de ce rapport. Presque tous les votes mis à jour, dans des États de toutes tailles et de toutes tendances politiques, suivent ce modèle statistique. Un très petit nombre d’entre elles, cependant, sont particulièrement aberrantes. Sur les sept mises à jour des votes qui suivent le moins ce modèle, quatre mises à jour individuelles – deux au Michigan, une au Wisconsin et une en Géorgie – ont été particulièrement anormales et influentes en ce qui concerne cette propriété et se sont toutes produites dans la même fenêtre de cinq heures.
En particulier, nous sommes en mesure de quantifier le degré de conformité à cette propriété et de découvrir que, sur les 8 954 mises à jour de vote utilisées dans l’analyse, ces quatre mises à jour décisives étaient les 1ère, 2ème, 4ème et 7ème mises à jour les plus anormales de l’ensemble des données. Non seulement chacune de ces actualisations de vote ne suit pas le modèle généralement observé, mais le comportement anormal de ces actualisations est particulièrement extrême. En d’autres termes, ces mises à jour de vote sont des aberrations parmi les aberrations.
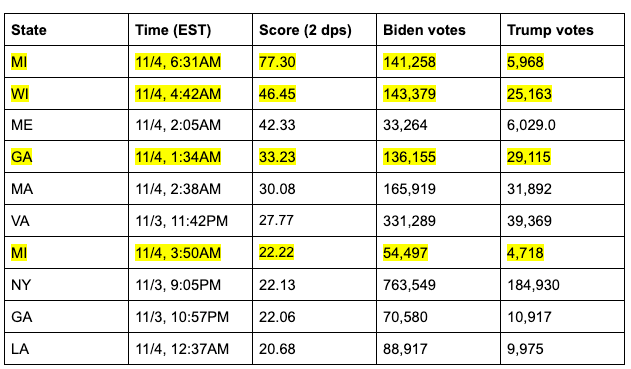
Les quatre mises à jour de vote en question sont :
- Une mise à jour de la liste du Michigan à 6 h 31, heure de l’Est, le 4 novembre 2020, qui indique 141 258 votes pour Joe Biden et 5 968 votes pour Donald Trump.
- Une mise à jour dans le Wisconsin à 3 h 42, heure centrale, le 4 novembre 2020, qui indique 143 379 votes pour Joe Biden et 25 163 votes pour Donald Trump.
- Une mise à jour des votes en Géorgie répertoriée à 1h34, heure de l’Est, le 4 novembre 2020, qui indique 136 155 votes pour Joe Biden et 29 115 votes pour Donald Trump.
- Une mise à jour de la liste du Michigan à 3 h 50, heure de l’Est, le 4 novembre 2020, qui indique 54 497 votes pour Joe Biden et 4 718 votes pour Donald Trump.
Ce rapport prédit ce à quoi ces mises à jour des votes auraient ressemblé, si elles avaient suivi le même schéma que la grande majorité des 8 950 autres. Nous constatons que l’ampleur des anomalies respectives est supérieure à la marge de victoire dans les trois États – Michigan, Wisconsin et Géorgie – qui représentent collectivement quarante-deux voix électorales.
De nombreux détails mathématiques sont fournis et les données et le code (pour le traitement des données, la transformation des données, le traçage et la modélisation) sont tous joints en annexe de ce document [1].
Contexte
À la fin de la nuit de l’élection 2020, le président Donald J. Trump avait une avance d’environ 100 000 voix dans le Wisconsin, une avance d’environ 300 000 voix dans le Michigan et une avance d’environ 700 000 voix en Pennsylvanie. Les calculs effectués à rebours ont montré que, pour dépasser le président Trump, Joe Biden devrait améliorer considérablement ses résultats dans les circonscriptions restantes, dont beaucoup se trouvaient dans des régions très bleues (c’est-à-dire démocrates, NdT) comme Détroit, Milwaukee et Philadelphie.
Le soir de l’élection, des informations contradictoires sont arrivées selon lesquelles divers bureaux de vote arrêtaient leur décompte pour la soirée, renvoyaient les agents électoraux chez eux ou recommençaient leur décompte. Une grande confusion persiste à ce jour quant à l’ampleur de l’arrêt du décompte dans les différents bureaux de vote, ainsi que sur la mesure dans laquelle les lois ou règles électorales de l’État ont été enfreintes en renvoyant les agents électoraux chez eux prématurément. Quoi qu’il en soit, plusieurs bureaux de vote du Wisconsin, du Michigan et de la Pennsylvanie ont continué à communiquer des chiffres tout au long de la nuit.
Dès les premières heures du matin suivant, le Wisconsin a basculé dans le bleu, tout comme le Michigan peu après. Quelques jours plus tard, la Géorgie et la Pennsylvanie ont fait de même. Compte tenu du contexte incertain, de nombreux observateurs et commentateurs américains se sont immédiatement montrés mal à l’aise ou sceptiques face à ces tendances.
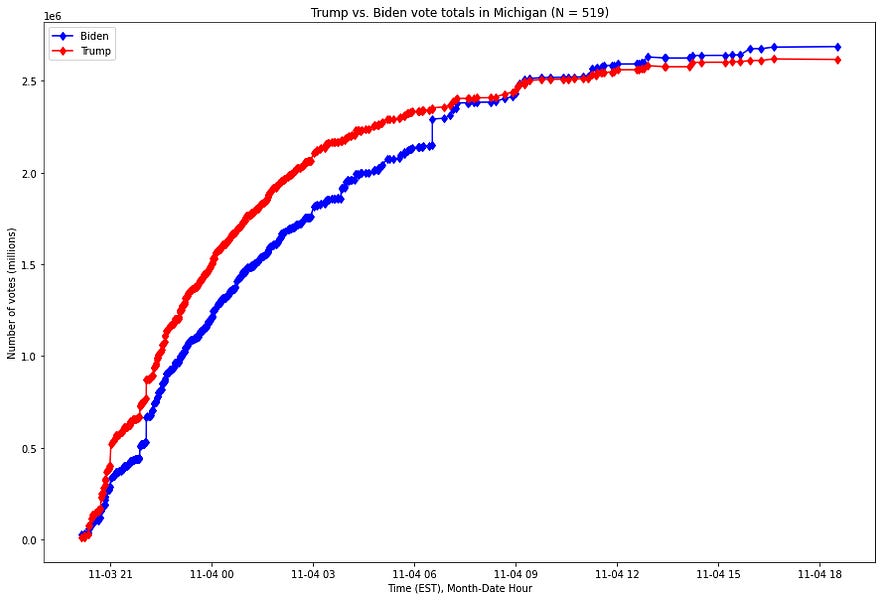
Pour le contexte, en utilisant les données publiquement disponibles du New York Times, voici une visualisation du nombre de votes par candidat dans le Michigan, du début de la nuit électorale jusqu’à 19 heures, heure normale de l’Est (EST), le 4 novembre 2020 :
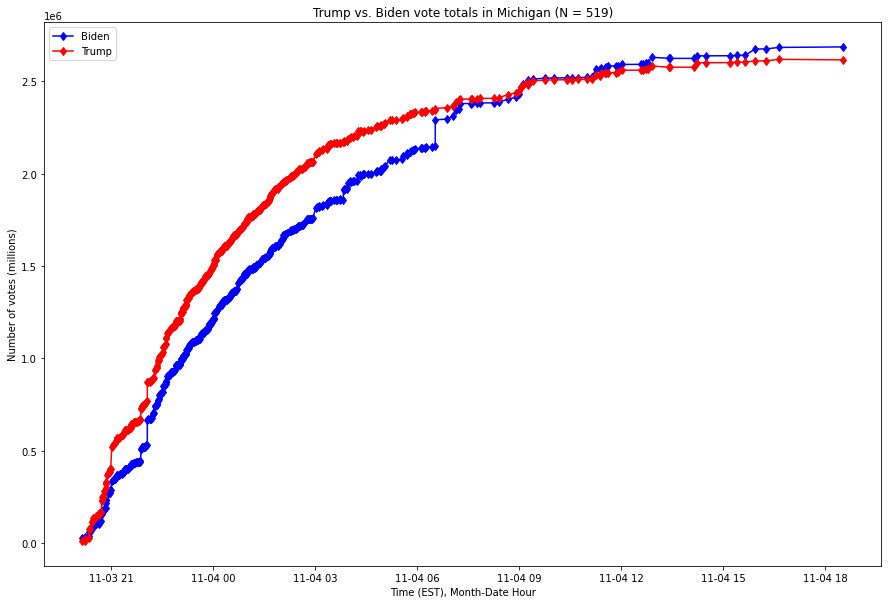
Comme le montre ce graphique, Joe Biden a dépassé l’avance du président Trump grâce à un petit nombre de mises à jour des votes qui ont été massivement en faveur de Biden dans le Michigan aux premières heures de la matinée du 4 novembre.
La situation dans le Wisconsin est encore plus frappante : une seule mise à jour du décompte des voix a permis à Biden de passer de la tête à la queue avec plus de 100 000 voix. Voici le graphique comparable, sur la même période, pour le Wisconsin, avec l’axe des x (temps) exprimé en heure normale centrale (CST) :
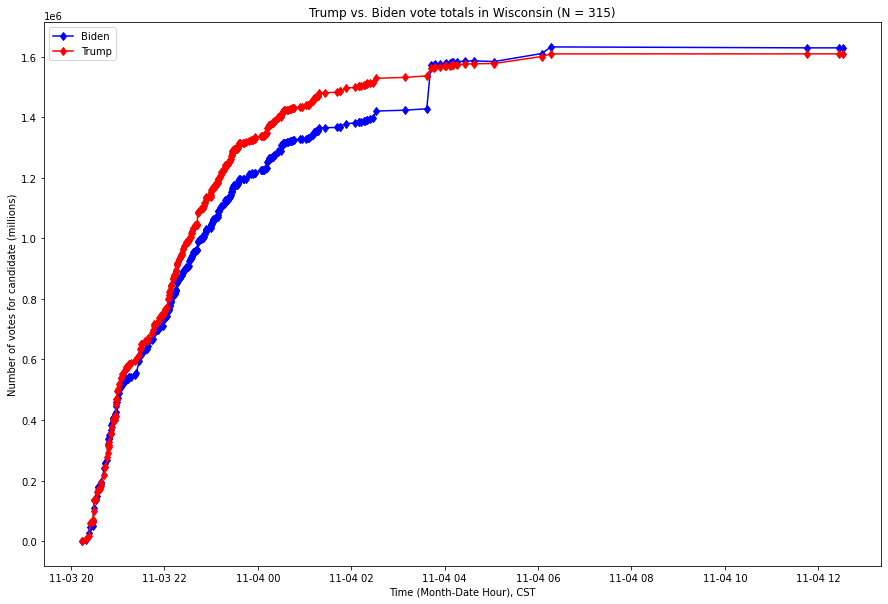
Différentes versions de ces graphiques ont suscité un débat en ligne. Alors que certains commentateurs ont fourni une analyse relativement partisane, d’autres ont simplement exprimé leur surprise face aux bonds quasi verticaux de certaines de ces mises à jour de votes. Ce phénomène est-il susceptible de se produire de manière organique ? Pour tenter de répondre à cette question, le présent rapport évalue le caractère extrême et inhabituel de ces pics par rapport à d’autres mises à jour des votes dans les États du Michigan, du Wisconsin et de la Géorgie, ainsi qu’à l’échelle nationale.
Grâce à plusieurs mécanismes d’enquête, nous constatons que ces quatre mises à jour de votes sont extraordinairement anormales. Bien qu’elles ne prouvent pas à elles seules l’existence d’une fraude ou d’un problème systémique, elles invitent à un examen plus approfondi.
Le concept, l’intuition et la mesure
L’analyse des données repose sur la reconnaissance et l’évaluation des modèles dans les données. Lorsque nous trouvons des données anormales, c’est souvent une indication de différences sous-jacentes. C’est pourquoi, dans ce rapport, nous nous concentrons sur ces quatre mises à jour de vote.
Il existe également un certain nombre d’intuitions générales sur lesquelles nous nous appuyons pour orienter nos recherches. En général, plus la taille de l’échantillon est grande, plus l’écart par rapport à la moyenne de la population devrait être faible. Bien que des rapports de vote anormaux puissent se produire, la probabilité statistique de marges anormales diminue à mesure que la taille de l’échantillon (ou la mise à jour des votes) augmente.
L’intuition de base est la suivante : les grandes marges sont une chose, tout comme les résultats très faussés, mais il est étrange d’avoir les deux en même temps, car ils sont généralement inversement liés lorsque l’une ou l’autre valeur augmente.
Nous démontrerons ci-dessous que les données suivent très majoritairement cette intuition, mais que quatre actualisations clés du vote identifiées par ce rapport vont à l’encontre de cette intuition.
En particulier, nous montrerons l’existence d’une relation inverse très forte au sein des mises à jour des votes, dans tous les États et à toutes les époques, entre la différence de votes pour Joe Biden et Donald Trump (souvent appelée ” marge Biden-Trump “) et le rapport entre les votes de Joe Biden et ceux de Donald Trump (souvent appelé ” rapport Biden:Trump “). Comme décrit plus en détail dans la section suivante, nous prenons le logarithme naturel des ratios afin qu’ils soient symétriques, c’est-à-dire que nous ne traitons pas les deux candidats différemment lors de la représentation graphique et de l’analyse. Ces valeurs sont souvent appelées “log-ratio Biden:Trump”. Le logarithme étant une transformation préservant l’ordre – c’est-à-dire que si x est plus grand que y, alors log(x) sera plus grand que log(y), et vice versa – nous les utilisons parfois de manière interchangeable lorsque la précision n’est pas requise.
À n’importe quel niveau géographique, nous pouvons tester l’hypothèse d’une relation inverse entre la taille de la mise à jour des votes et l’extrémité du rapport entre les votes des candidats, et, comme nous le verrons ici, la relation est extrêmement forte. Dans les États rouges et bleus, où la participation est élevée et faible, il existe une relation inverse évidente entre les deux.
Mesurer cette relation entre la marge du candidat et son ratio
Essayons maintenant de quantifier la nature de la relation inverse dans le contexte d’un état particulier. Tout d’abord, nous prenons notre ensemble de données sur les totaux de votes courants[2] pour chaque état, et, pour chaque état, nous calculons la différence de votes pour chaque candidat entre les mises à jour. Cela produit une séquence de différences de vote, dont la somme, dans un état donné, est le total.
Pour commencer, nous considérons chaque mise à jour séquentielle dans l’État du Michigan où les totaux des votes pour Trump et Biden sont supérieurs à zéro [3]. Pour chacun d’entre eux, nous calculons deux valeurs :
- La différence entre le nombre de votes pour Biden et le nombre de votes pour Trump – la “marge”.
- Le logarithme [4] du rapport entre le nombre de votes pour Biden et le nombre de votes pour Trump – le “log-ratio”.
Remarque : ces deux métriques sont symétriques. Si nous considérons que f1 est la première métrique et f2 la seconde, le lecteur remarquera que, pour tout nombre positif (X, Y) :
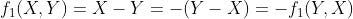
Et ça :
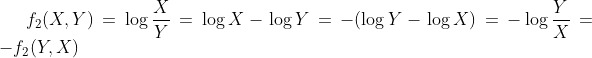
En d’autres termes, étant donné X pour Biden et Y pour Trump, l’une ou l’autre métrique produira un score opposé à celui qu’elle produirait si la mise à jour avait plutôt Y voix pour Biden et X pour Trump. Cette propriété est extrêmement utile et sera mise à profit lors de l’analyse statistique.
Les lecteurs pourraient se demander : pourquoi mesurez-vous le ratio ? Pourquoi ne pas mesurer la différence entre les proportions de votes (ou, de manière équivalente, leurs pourcentages). La réponse à cette question réside dans ce que nous recherchons, c’est-à-dire des preuves de fraude ou d’irrégularité qui se manifestent par des résultats extrêmement inhabituels. En particulier, les ratios ne sont presque jamais utilisés pour exprimer le nombre de votes (on entend généralement parler de pourcentages ou, lorsqu’une élection est serrée, de chiffres) et, par conséquent, toute personne qui commet une fraude et cherche à “couvrir ses traces” est plus susceptible de “jouer” avec les mesures auxquelles elle est habituée et beaucoup plus susceptible de laisser des traces dans les mesures qu’elle ne prend pas en compte.
Cela masque des différences essentielles entre les deux statistiques.
- Les ratios démontrent une propriété importante : plus l’avance d’un candidat est grande, plus il est difficile de faire progresser le prochain 1 %. Ils reflètent la difficulté relative de chaque vote marginal à mesure que le nombre de votes restants diminue. Ils reflètent la difficulté relative de chaque voix marginale à mesure que le nombre de voix restantes diminue. Lorsqu’un candidat s’approche de 0 ou 100 % des voix, les taux auxquels le rapport entre les voix de ce candidat et celles des autres candidats converge vers zéro ou l’infini sont très différents.
- Les ratios nous permettent de repérer un signe potentiel de fraude : des ratios anormalement bas entre le candidat (principal) perdant et d’autres candidats moins connus. Comme ceux qui observent les élections et y participent ont tendance à ne pas penser en ces termes, s’il y a fraude, il est beaucoup moins probable qu’ils aient couvert leurs traces à cet égard. Une élection de type dictateur de pacotille où le candidat favori obtient 99 % des voix est évidemment suspecte, mais on accorde souvent moins d’attention à des détails tels que le rapport entre le candidat perdant le plus populaire et les candidats tiers de longue date. L’examen de métriques moins populaires dans la pratique sera extrêmement utile ici, comme nous le verrons.
Pour illustrer cela, considérons une séquence de deux élections hypothétiques entre Tom et Harry. Imaginez que la première fois, Tom gagne avec 55 % des voix contre 45 % pour Harry. Quatre ans plus tard, Harry est le challenger et Tom améliore sa marge à 60 % des voix. Cela peut se produire de plusieurs façons : conquête de nouveaux électeurs, abandon des partisans d’Harry, report des partisans d’Harry sur Tom, ou une combinaison de tous ces facteurs. Considérons simplement le dernier cas pour le moment. Pour que Tom passe de 55% à 60%, il doit convertir un partisan de Harry sur neuf, soit un peu plus de 11%. Ce n’est peut-être pas facile, mais c’est tout à fait possible.
Considérons maintenant une autre élection hypothétique dans un électorat fortement partisan, entre Alice et Bob. Lors de la première élection, Alice obtient 90% et Bob 10%. Pour qu’Alice obtienne le même pourcentage absolu d’augmentation que Tom, c’est-à-dire 5%, elle doit convertir 5% d’une population de 10%. En d’autres termes, elle doit convertir un partisan de Bob sur deux. Pour des raisons qui sortent du cadre de cet article, cela n’est peut-être pas 4,5 fois plus difficile que pour un candidat qui passe de 55% à 60% du total des votes, mais c’est sans aucun doute beaucoup plus difficile. Un exemple utile est celui de San Francisco, en Californie, qui, bien qu’étant l’une des villes les plus bleues d’Amérique numériquement et culturellement, est une ville où les candidats démocrates à la présidence obtiennent régulièrement environ 90 % des voix, mais ne semblent jamais atteindre 95 %. Il y a des républicains à San Francisco, mais ils sont peu nombreux, et en convertir la moitié est un défi de taille. Cela fait des ratios un outil utile dans notre arsenal pour répondre aux questions du type “combien serait trop” ? Cela nous permet d’évaluer les données d’une manière qui, selon nous, est qualitativement différente – et qualitativement supérieure – aux formes d’évaluation courantes utilisées par les individus moyens et les médias d’information.
Cette élection représente une occasion extraordinaire et unique pour les analystes de l’intégrité électorale et l’application de la recherche statistique sur la détection de la fraude, car il s’agit probablement de la première élection nationale de l’histoire américaine, à tout le moins, où le grand public a eu accès à des données électorales en série chronologique. Même les articles universitaires respectés qui étudient la fraude électorale dans d’autres pays[6] semblent étudier principalement des informations après coup sur les décomptes finaux ; l’analyse est faite sur la base de statistiques sur la participation électorale, la fréquence des chiffres et d’autres informations qui sont disponibles dans les chiffres officiels après coup. Après tout, si l’on en croit les rapports faisant état d’une fraude et d’une corruption généralisées ordonnées par le sommet lors des élections en Russie, en Ouganda, en Ukraine, en Iran, etc., il est peu probable que ces gouvernements, qui ont tendance à avoir beaucoup plus de contrôle sur ce qui peut et ne peut pas être publié que notre gouvernement, veuillent augmenter le nombre de dimensions sur lesquelles leur prétention à la légitimité peut être vérifiée.
Un regard sur le Michigan
Calculons maintenant ces deux valeurs pour chaque mise à jour des votes dans le Michigan où Biden et Trump ont tous deux des valeurs positives. Si l’on suit l’intuition selon laquelle il existe une relation inverse entre les marges d’une mise à jour et son ratio, nous devrions nous attendre à voir un grand groupe de données avec quelques points au-dessus, au-dessous, à gauche et à droite, et pratiquement aucun point en haut à droite (qui représenterait une marge Biden-Trump et un ratio Biden:Trump simultanément extrêmes) ou en bas à gauche (qui est analogue mais favorable à Trump).
Voici cette distribution, présentée sous forme de nuage de points, avec les marges numériques en abscisse et les log-ratios en ordonnée.
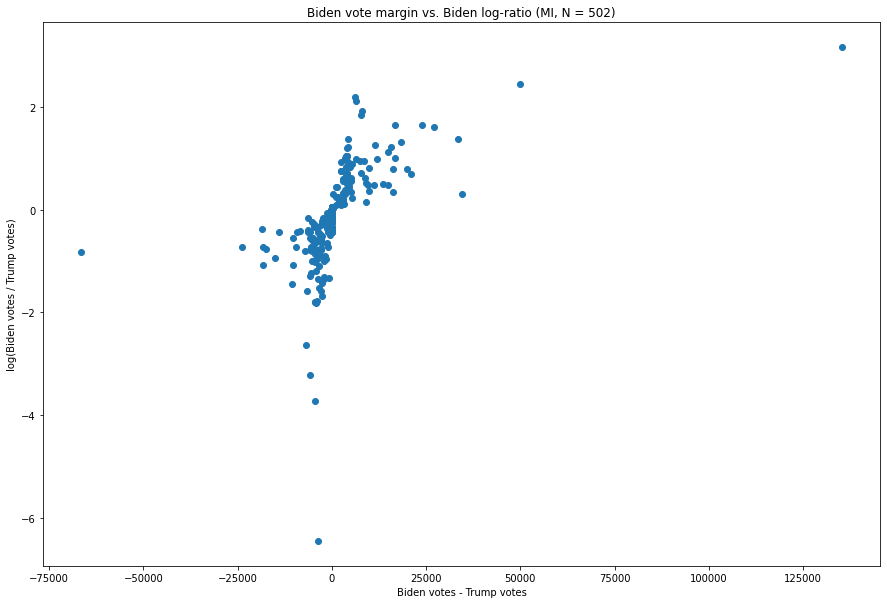
Comme nous pouvons le constater, la plupart des observations suivent le contour de base de notre hypothèse, c’est-à-dire que plus une mise à jour est extrême à un égard, moins elle l’est à un autre.
Par exemple, la mise à jour à (-3,622, -6.449), présente un ratio assez extrême de votes Biden:Trump – environ 1:632 – mais n’est pas très importante, ne produisant qu’une marge de -3 622 votes pour Biden, ce qui, comme nous pouvons le voir, n’est pas terriblement extrême dans le contexte de cette distribution. De même, le point situé tout à gauche (-66 456, -0,816) est un point où la marge de Biden est importante (-66 546), mais où le rapport, d’environ 1:2,26, n’est pas particulièrement inhabituel pour une mise à jour des votes en faveur de Trump.
Nous pouvons également observer ce schéma dans presque toutes les mises à jour favorables à Biden. Par exemple, la mise à jour présentant la troisième plus grande marge pour Biden, à (34 450, 0,296), compte 134 326 votes Biden contre 99 867 votes Trump, et présente un rapport Biden:Trump de 1,34:1 seulement. Et la mise à jour présentant le troisième plus grand rapport Biden:Trump, à (6 091, 2,184), dans laquelle Biden a reçu 6 863 voix et Trump 773 voix, présente un rapport assez extrême de 8,884 mais ne rapporte à Biden que 6 091 voix, un chiffre relativement faible par rapport à ce que nous allons examiner ensuite.
Deux points ressortent.
Considérons tout d’abord le moins extrême d’entre eux, c’est-à-dire le point à (49 779, 2,447). Ce point, qui représente une mise à jour des votes de 54 497 pour Biden et de 4 718 pour Trump et qui est arrivé à 3 h 50 ET le 4 novembre 2020, représente à la fois la deuxième plus grande marge de vote de Biden, avec 49 779, et le deuxième plus grand ratio Biden:Trump, avec 11,55:1. Comme nous pouvons le voir et comme décrit ci-dessus, la mise à jour ayant la plus grande marge suivante était une mise à jour avec seulement 7 776 votes, alors que cette mise à jour avait plus de 7 fois plus de votes et était plus fortement en faveur de Biden.
L’étrangeté de la mise à jour décrite ci-dessus n’est toutefois pas comparable à celle de la mise à jour située dans le coin supérieur droit. Cette mise à jour, à (135 290, 3 164), représente la mise à jour des votes décrite au début de ce rapport, et est responsable du pic extrêmement remarquable qui a presque éliminé l’avance de Trump en un seul coup. Elle est arrivée à 6h31 ET le 4 novembre, et est passée de 141 258 pour Biden à 5 968 pour Trump – représentant à la fois la plus grande marge de voix pour Biden parmi les 502 mises à jour que nous avons ici, à 135 290, et représentant également, par un facteur de plus de 2, le plus grand ratio Biden:Trump, avec un énorme 23,67:1 (dont le logarithme est 3,16). Comme nous le verrons lors de la comparaison avec d’autres États, il s’agit, selon nos critères, du point le plus anormal du pays.
Cette mise à jour est aussi particulièrement intéressante pour une autre raison : il y a 2 546 votes hors parti, alors que Donald Trump n’en a que 5 968. Voici un histogramme du rapport entre le nombre total de voix et le nombre de voix des autres partis, pondéré par Trump [7] :
Comme nous le voyons, lorsque nous pondérons par le nombre de votes dans une mise à jour donnée, cette mise à jour est particulièrement anormale. Le ratio suivant le plus proche pondéré par le nombre de votes est inférieur aux deux tiers de celui-ci, et la médiane – 137,56 – est inférieure d’un facteur d’environ 464,5. Il est évidemment très surprenant qu’un lot de votes aussi important soit compté tout en montrant une performance aussi exceptionnellement faible de Trump par rapport au vote des autres partis.
En particulier, elle remet sérieusement en question la véracité de cette mise à jour des votes, et constitue peut-être l’une des preuves directes de fraude les plus solides de tout ce rapport. Une personne cherchant à améliorer frauduleusement les marges de Joe Biden par rapport à Donald Trump cherchera probablement à couvrir ses traces en maintenant la part de Joe Biden dans la mise à jour à une valeur raisonnable. 95 % peut sembler plausible, mais 99,9 % à cette échelle devient à première vue invraisemblable pour tout observateur honnête. Un moyen efficace d’atteindre l’objectif souhaité, à savoir réduire l’avance de Donald Trump à ce stade, aurait été de supprimer le vote Trump tout en gonflant artificiellement le vote sans parti dans le but de dissimuler à quel point cette mise à jour était favorable à Biden. En fait, c’est précisément la raison pour laquelle ce rapport utilise des ratios : comme il s’agit d’une mesure qui n’est pratiquement jamais utilisée dans un but pratique pour discuter des résultats électoraux, une personne qui commet une fraude est beaucoup moins susceptible de tenir compte de l’aspect inhabituel d’un ratio. En particulier, parce que les candidats sans parti ont reçu beaucoup moins d’attention médiatique que lors de l’élection présidentielle de 2016, et que le candidat du Parti vert a même été suivi avec succès lors du scrutin dans un ou plusieurs États, il est difficile de croire que cette mise à jour du vote n’a favorisé Trump sur le vote sans parti que par un facteur inférieur à 2,5, alors que le ratio à l’échelle de l’État était supérieur à 31[8].
En l’absence d’une explication convaincante de la raison pour laquelle cette mise à jour particulière – à un moment si crucial, dans un État crucial, qui a amélioré la position de Biden dans l’État de façon si spectaculaire – a également eu des résultats si inhabituels pour les votes sans parti par rapport aux votes de Trump, il semble peu probable que cette mise à jour des votes reflète une comptabilité honnête des votes légitimes.
Les sections suivantes du présent rapport quantifient le degré d’extrémisme à d’autres égards et examinent les implications d’un degré d’extrémisme légèrement inférieur.
Un regard sur le Wisconsin
Voici le graphique analogue pour le Wisconsin.
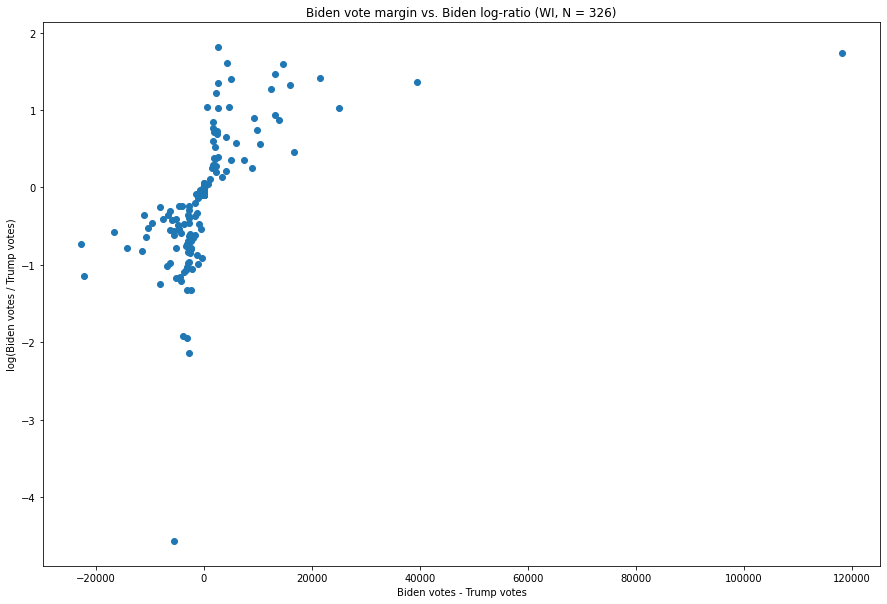
Les tendances de ce graphique sont un peu plus étranges. Les mises à jour favorables à Trump (c’est-à-dire celles situées à gauche de zéro sur l’axe des x) présentent une relation inverse entre la marge de victoire dans une mise à jour favorable à Trump et le rapport entre les votes Trump et Biden. Par exemple, la mise à jour à (-5,433, -4,564), qui est la plus extrême de l’État en termes de rapport, provient d’un lot de bulletins exceptionnellement favorable à Trump, qui a donné 5 490 voix pour Trump et 57 pour Biden, soit un rapport Trump:Biden d’environ 96:1 pour Trump. Ce chiffre en lui-même est assez élevé, mais, surtout, il n’est pas anormal par rapport à la forme de la distribution. Le signe révélateur de la bizarrerie ici n’est pas l’extrémité par rapport à l’une ou l’autre valeur, mais la co-extrémité.
La répartition de Biden semble un peu bizarre ici, mais il y a un point qui ressort particulièrement, à savoir celui en haut à droite, à (118,215, 1,74). Il s’agit de la mise à jour des votes qui est arrivée à 3 h 42 CST le 4 novembre, et qui donnait 143 379 pour Biden contre 25 163 pour Trump [9], ce qui donne une marge de 118 215 et un rapport Biden:Trump d’environ 5,7:1 – soit environ 3 fois plus que la mise à jour avec la marge la plus importante suivante (qui était de 39 499). Dans le même temps, une seule mise à jour – une mise à jour avec seulement 6 435 voix (soit environ un facteur 18 de moins que la mise à jour en question) qui a donné 3 037 voix à Biden contre 495 à Trump – présente un ratio plus important, de l’ordre de 6,14:1.
Un regard sur la Géorgie
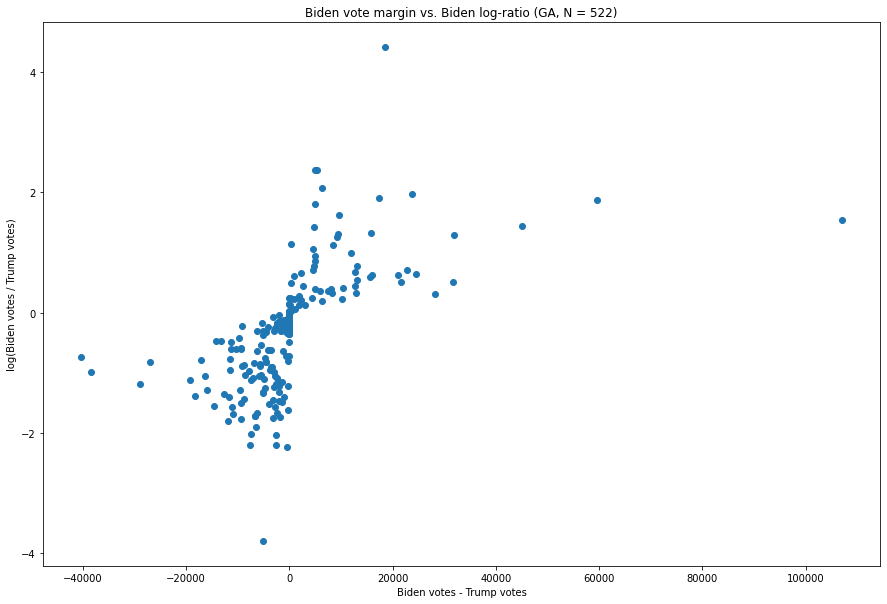
Celui-ci ne semble que légèrement plus anormal que les autres graphiques de ce type, mais, comme nous allons le voir, il contient en fait deux des neuf mises à jour de votes les plus anormales de notre distribution combinée de 8,954 mises à jour de votes. En particulier, le point situé à (136,155, 1,543), représentant une mise à jour des votes arrivée à 1 h 34 EST le 4 novembre, est la mise à jour présentant la plus grande marge de toutes les mises à jour en Géorgie – elle présente également le 10e plus grand rapport Biden:Trump. Il y a quelques mises à jour plus petites avec des ratios plus extrêmes, mais, comme nous le détaillons plus loin dans ce rapport, ce point est en fait inhabituel.
Un bref aperçu des autres États
Nous nous tournons maintenant vers d’autres États, en particulier ceux qui présentent des caractéristiques similaires (par exemple, un État ” clé “, c’est-à-dire dans lequel un ou deux noyaux urbains à dominante démocrate compensent une population par ailleurs très républicaine). Cela nous aide à établir une base initiale de ce à quoi ces distributions devraient ressembler dans un État avant de commencer à comparer les mises à jour directement entre les États.
Pennsylvanie :
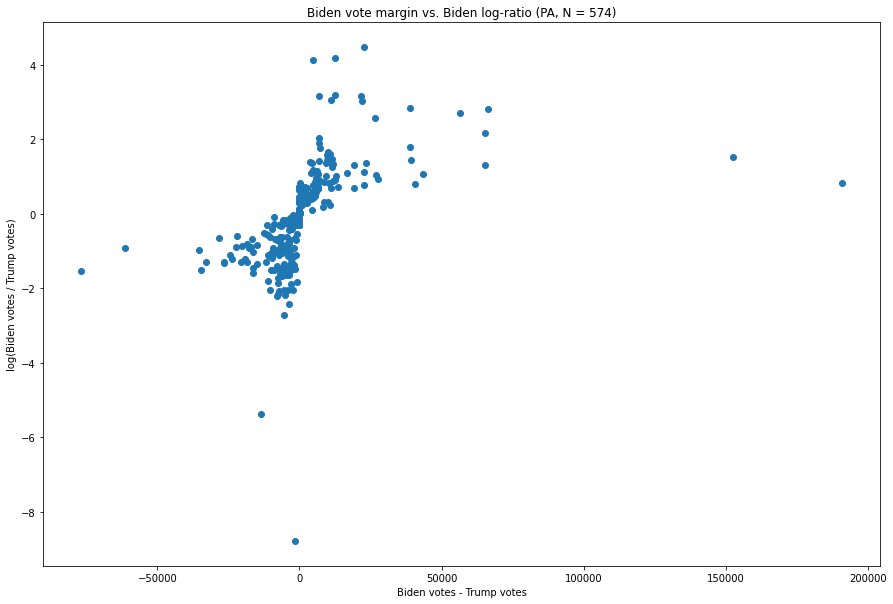
La relation inverse est immédiatement visible ici. Nous avons des points près du bas (représentant des ratios élevés de votes Trump:Biden), quelques points loin sur la gauche (représentant des valeurs élevées de Trump – Biden), et un couple (beaucoup plus loin) sur la droite, représentant une marge élevée de Biden-Trump, mais qui ne sont pas particulièrement extrêmes en termes de ratio Biden:Trump.
Minnesota :
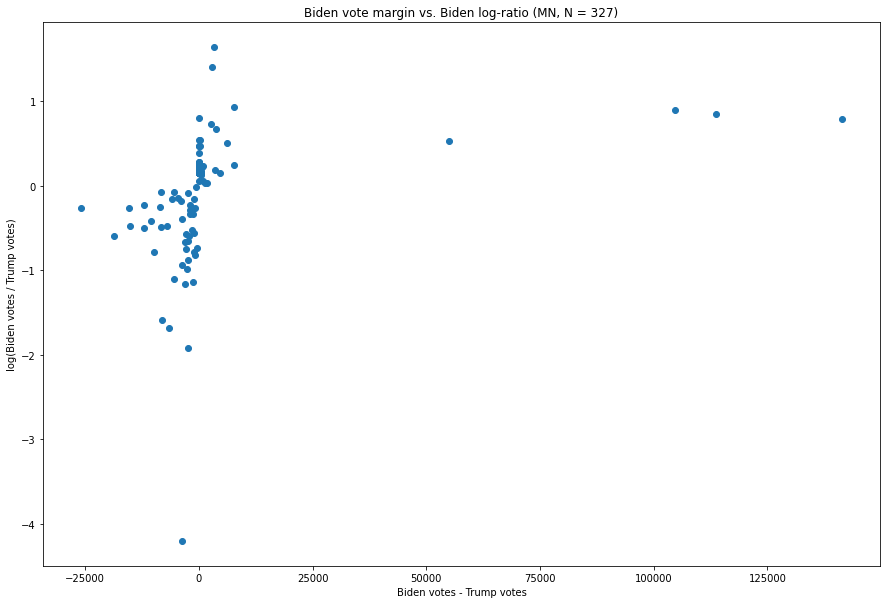
Bien qu’il y ait une mise à jour plus extrême en termes de ratio Trump:Biden, et plusieurs mises à jour avec des marges Trump-Biden extrêmement importantes, nous voyons que la forme de base reste la même.
New York :
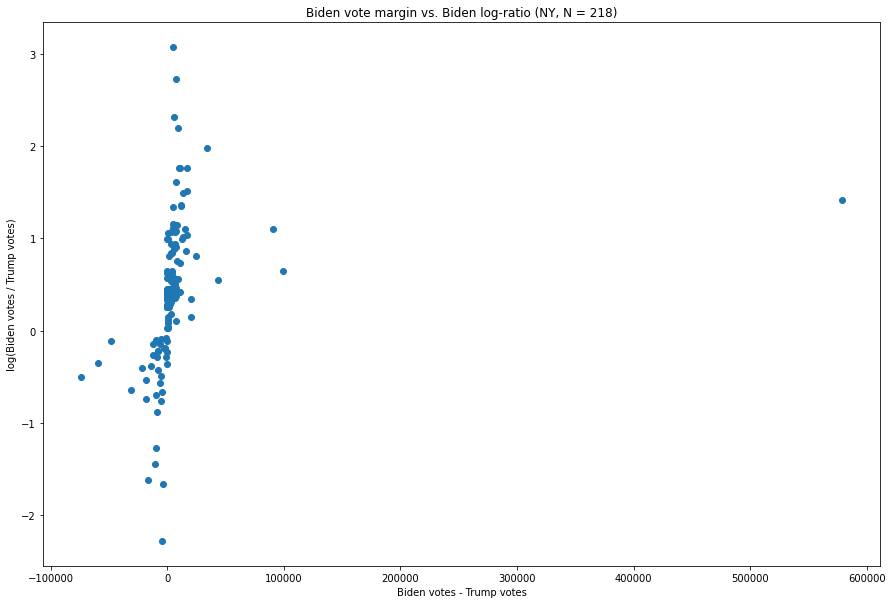
Les marges de vote pour chaque mise à jour sont assez fortement concentrées autour de zéro, tandis que les quelques mises à jour qui ont des marges exceptionnellement importantes pour l’un ou l’autre candidat ont des ratios qui ne sont pas aussi extrêmes que ceux de nombreuses autres mises à jour.
Consolider, comparer et mesurer
Après avoir fait un bref tour des États présentant des caractéristiques similaires, c’est-à-dire où Joe Biden est actuellement en tête et où le vote démocrate provient en grande majorité d’une seule zone urbaine (ou peut-être de deux, dans le cas de la Pennsylvanie), nous pouvons constater que les graphiques du Michigan et du Wisconsin semblent tous deux inhabituels. Afin d’évaluer plus rigoureusement dans quelle mesure cette situation est réellement anormale, il est nécessaire de tenir compte du fait que la marge typique Biden-Trump et le ratio Biden:Trump varient considérablement d’un État à l’autre. Si nous nous contentons de prendre ces valeurs telles quelles, la plupart des différences entre, par exemple, l’Alabama et la Californie ne seraient probablement que des artefacts des écarts considérables entre les performances des candidats dans ces États.
Pour y parvenir, nous pouvons utiliser un processus de transformation des données appelé normalisation. Il s’agit d’un processus par lequel, pour une série de données numériques, la moyenne des données est soustraite de chaque point, puis le résultat est divisé par l’écart-type. On obtient ainsi une série de distributions qui permettent de comparer ces valeurs (c’est-à-dire la marge Biden-Trump par date de vote et le log-ratio Biden:Trump) entre des États de taille et de tendance politique très différentes. La normalisation des données est une technique très courante dans le domaine de l’apprentissage automatique pour entraîner des modèles sur des ensembles de données ayant des magnitudes et des moyennes numériques très différentes [10], car elle fournit précisément la fonctionnalité dont nous avons besoin ici.
Nous pouvons donc normaliser chaque point individuel (marge, log-ratio) dans son état [11], et le tracer comme nous l’avons fait auparavant. Voici à quoi ressemble ce graphique. Les valeurs pour le Michigan sont en rouge, celles du Wisconsin en vert, et celles de tous les autres États en bleu :
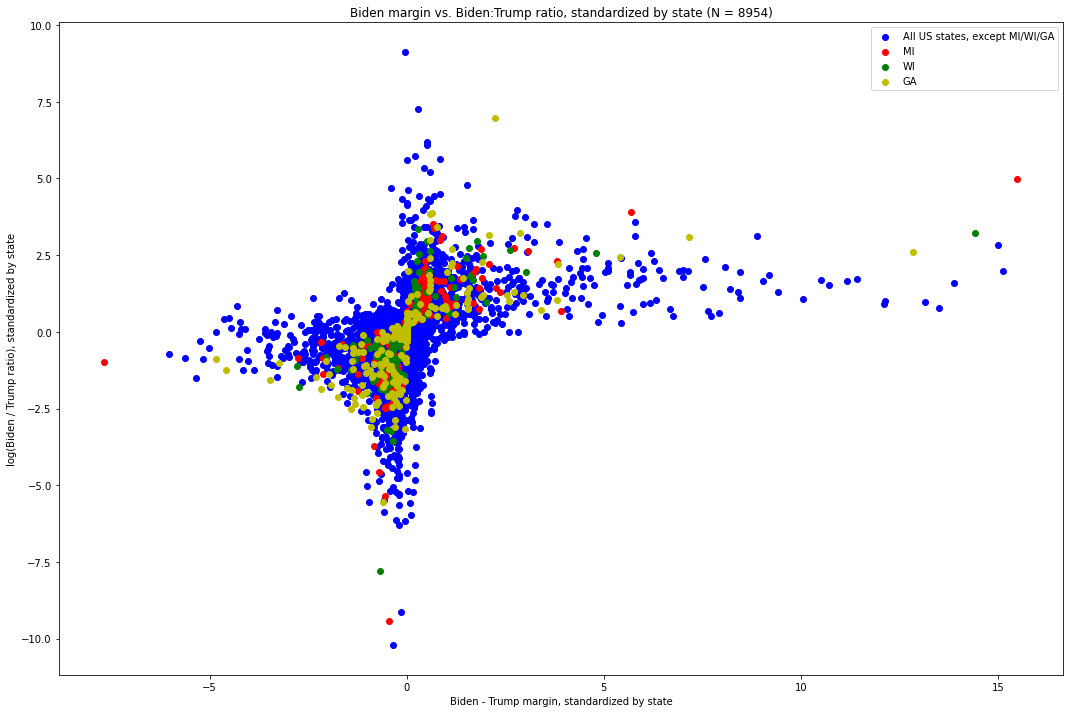
Sur ces 8 954 mises à jour de votes à travers le pays, nous pouvons voir à quel point le modèle est écrasant. En particulier, nous constatons que – à quelques exceptions notables près – lorsqu’une valeur devient plus extrême dans une direction donnée, l’autre tend à devenir moins extrême.
Cela nous amène aux exceptions visuellement identifiables.
Si nous portons notre attention sur les points situés à l’extrémité droite de la distribution, c’est-à-dire ceux qui présentent la marge Biden-Trump la plus extrême par rapport à leur État, nous voyons immédiatement un point du Michigan, qui se situe bien au-dessus de ce que la forme du graphique aurait pu laisser prévoir. Ce point, situé à (15,494, 4,989), correspond à la mise à jour des votes qui est arrivée à 6 h 31 EST le 4 novembre et qui a donné 141 257 voix à Biden et 5 968 à Trump. Rappelons que cette mise à jour avait à la fois la plus grande marge (135 290) de toutes les 574 mises à jour[12] dans le Michigan, d’environ 85 000 voix, et un facteur d’environ 2,7 par rapport à la mise à jour la plus importante suivante, (5,679, 3,912) – qui, de manière critique (et surprenante, par rapport à ce que montre cette distribution), était à la fois la deuxième plus importante en termes de marge Biden-Trump et de ratio Biden:Trump[13]. Elle présentait également le ratio Biden:Trump le plus élevé (environ 23,69:1), soit un facteur de plus de 2 par rapport à la mise à jour présentant le ratio Biden:Trump le plus élevé suivant. L’écart visuel entre cette mise à jour et le modèle dominant suivi par les autres mises à jour est flagrant, et nous allons bientôt quantifier à quel point il est extrême.
Ensuite, considérez le point vert situé juste un peu plus bas et à gauche de l’aberration rouge. Il s’agit de la mise à jour des votes dans le Wisconsin arrivée à 3 h 42 CST le 4 novembre, qui a donné 143 379 pour Biden et 25 163 pour Trump, soit une marge de 118 215 [14]. Il s’agit de la mise à jour présentant la plus grande marge Biden – Trump dans le Wisconsin, et de loin [15]. En termes de ratio Biden:Trump, elle est la deuxième plus importante – juste derrière une mise à jour 26 fois plus petite et pourtant à peine plus extrême dans son ratio [16].
Nous voyons également un point rouge à (5,679, 3,912), qui correspond à la mise à jour des votes qui est arrivée à 3h50 EST le 4 novembre et qui est passée de 54 497 pour Biden à 4 718 pour Trump, soit une marge de 49 779 et un ratio de 11,55:1. Il convient de noter que, bien qu’elle ne soit pas aussi anormale que la mise à jour de 6 h 31 EST, cette mise à jour était très extrême dans les deux domaines. Toutefois, comme nous le verrons, il s’agit de la septième valeur la plus extrême en termes de non-adhésion à la distribution dans son ensemble.
Bien que ces deux points soient inhabituels en soi, il est exceptionnellement improbable qu’ils proviennent du même État, d’une importance cruciale pour l’élection, à moins de trois heures d’intervalle au cours d’un processus de dépouillement de nuit – un processus sujet à une grande controverse et où il reste, près de trois semaines après le jour de l’élection, de nombreuses inconnues. Ensemble, ces deux mises à jour des votes ont fourni à Joe Biden les voix nécessaires pour lui donner l’avantage dans cet État.
Quantification de l’extrémité
Après avoir démontré visuellement à quel point les quatre mises à jour des votes clés sont anormales, nous pouvons maintenant tenter de quantifier à quel point il est inhabituel que ces trois points existent en même temps et que deux d’entre eux proviennent du même État.
Le graphique ci-dessous présente deux propriétés visuelles particulièrement intéressantes :
- Le graphique est présenté en deux dimensions, mais il est en réalité tridimensionnel. Il est visiblement beaucoup plus dense au centre, présente ce qui ressemble à deux distributions normales, et plus on s’éloigne de l’origine le long d’une ligne à pente positive qui passe par l’origine, plus la densité est faible.
- Les “bords” extérieurs du graphique, dans les quadrants supérieurs droits et inférieurs gauches, ressemblent beaucoup à la forme de la droite y = 1/x.
De même, nous nous attendons à ce que les points se trouvent dans les quadrants supérieur droit et inférieur gauche, et entre une ligne extérieure ayant la forme y = 1 / x et l’origine. Puisque ces valeurs seront donc le plus souvent soit négatives, soit positives, nous pouvons voir que la multiplication de la coordonnée x de chaque point par sa coordonnée y est un moyen utile d’évaluer dans quelle mesure il suit ce type de distribution. Puisqu’il y a plus de points près de l’origine que sur les “lignes de démarcation” visibles (c’est-à-dire les séquences de points sur les bords extérieurs dans les premier et troisième quadrants qui forment visiblement ces lignes qui ressemblent à un graphique, peut-être mis à l’échelle, de y = 1/x).
Ainsi, pour chaque paire de coordonnées (à nouveau, toutes deux standardisées par État) de la marge Biden-Trump et du log-ratio des votes Biden/Trump, nous pouvons multiplier ces valeurs et examiner la distribution des produits résultants. Ici, plus une valeur est importante en magnitude, moins elle suit la non-coextrémité. Le tracé de ces produits nous donne :
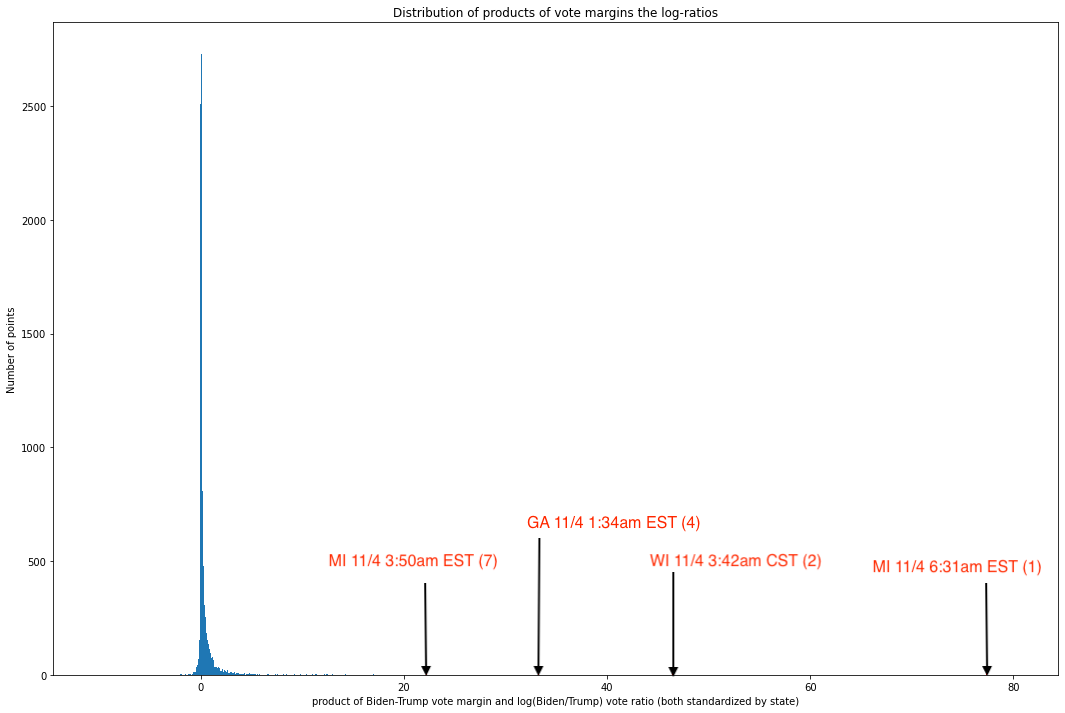
Comme nous pouvons le constater, les valeurs sont concentrées de manière écrasante près de la médiane, et le graphique est profondément incliné vers la droite – sinon, l’axe des x n’aurait pas besoin de s’étendre jusqu’à 80. Toutes les mises à jour, sauf 60 sur 8 954, ont des valeurs inférieures à 10, et toutes les mises à jour, sauf 10, ont des valeurs inférieures à 20. En d’autres termes, une part écrasante de mises à jour semble suivre cette règle de près, mais un petit nombre de mises à jour sont vraiment des aberrations extrêmes.
Une rapide plongée dans ces dix points révèle des données qui, à ce stade du rapport, seront très familières au lecteur :
Comme nous pouvons le constater, quatre des sept mises à jour de vote les plus anormales – c’est-à-dire les mises à jour dans lesquelles la marge et le ratio sont co-extrêmes – se situent dans des États où les élections sont critiques et ont eu lieu au cours de la même période de cinq heures où les circonstances sur le terrain étaient (et restent) contestées et hautement suspectes.
Il convient de noter ici qu’environ 15 % des mises à jour des votes dans l’ensemble des 8 954 données provenaient de ces trois États. Si nous supposons qu’il est également probable qu’un État particulier se retrouve à l’un de ces points extrêmes, il y aurait environ 1,2 % de chances que trois États soient représentés dans trois des quatre ou quatre des sept premières places, et environ 0,99 % de chances que ces trois États occupent cinq des sept premières places. Il est donc très surprenant de voir les États en question être représentés de façon si disproportionnée dans les 0,11 % supérieurs de la distribution de la coextrémité[17].
Prévision de résultats plus typiques et évaluation de leurs implications
Nous allons maintenant nous demander à quel point ces actualisations de votes devaient être extrêmes pour que Biden gagne ces États.
Pour ce faire, nous considérons des “ensembles de niveaux”[18] des produits des valeurs x et y des coordonnées que nous traçons, et nous considérons les percentiles de ceux-ci (par rapport aux valeurs tracées à la Fig. 10). Chaque ensemble de niveaux est un point dans cette distribution, et a un percentile correspondant. Par exemple, le 99e percentile des produits est d’environ 6,6 – bien plus petit que les valeurs de 77,30, 46,45, 33,23 et 22,22 que nous voyons pour ces quatre mises à jour. Nous pouvons maintenant déterminer à quoi aurait pu ressembler chacune de ces mises à jour si elles n’étaient qu’au 99e (ou autre) percentile de coextrémité. Pour ce faire, nous devons nous demander ce qui est le plus logique. Maintenir la marge constante et voir à quoi ressemblerait le ratio, ou maintenir le ratio constant et voir à quoi ressemblerait la marge ? Cette dernière option est beaucoup plus logique dans ce scénario, puisque la première suggère qu’un nombre égal de bulletins pour les deux candidats a pu être retenu de manière inappropriée, tandis que la seconde suggère probablement qu’un nombre excessif de bulletins pour le candidat gagnant a été produit. Nous sommes intéressés par le test de ce dernier scénario.
Puisque nous utilisons des ratios pour prédire les marges, il est logique de montrer ce à quoi ressemble le graphique de la figure 10 lorsque les axes sont inversés, afin de voir comment les marges varient avec le ratio.
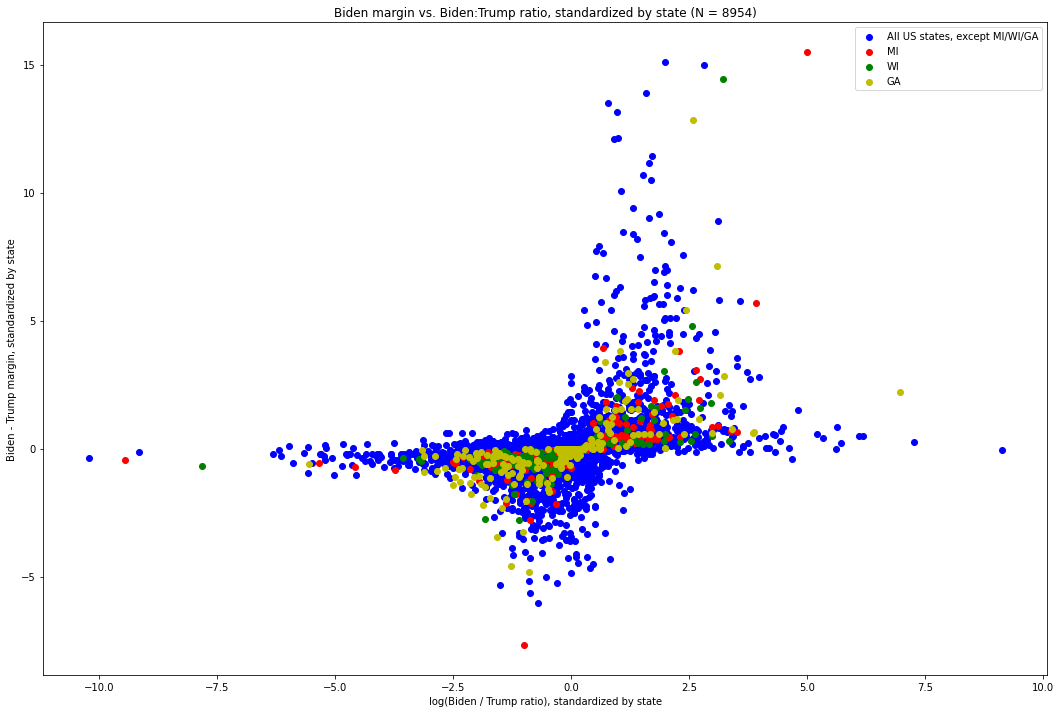
Les données sont les mêmes que celles de la figure 10, mais la présentation est plus naturelle pour l’utilisation des ratios afin de prédire les marges. Le modèle devient un peu plus clair lorsque nous regardons simplement les valeurs absolues, car nos examens ultérieurs reposent sur des mesures qui traitent les mises à jour des votes pro-Biden et pro-Trump de manière symétrique.
Nous pouvons également considérer l'”ensemble de niveau” des combinaisons (marge, ratio) qui forment un percentile particulier de coextrémité. Ici, nous montrons les valeurs absolues du rapport logarithmique (normalisé) et de la marge, avec les annotations de l’ensemble de niveaux pour les 95e, 99e et 99,5e percentiles :
Cela nous permet de voir clairement à quel point les mises à jour des votes sont extrêmes, par rapport à la propriété généralement observée selon laquelle elles sont délimitées par une courbe inverse [19]. La ligne noire pleine représente le 95e percentile — c’est-à-dire que 95 % des mises à jour des votes sont à l’intérieur de cette courbe (c’est-à-dire qu’elles ont des marges et des ratios moins coextrêmes). La ligne noire centrale, avec des tirets et des points, représente le 99e percentile, c’est-à-dire que 99 % des 8 954 mises à jour des votes sont moins coextrêmes que n’importe quel point de cette ligne. Et la ligne la plus haute (pointillés noirs) représente le 99,5ème percentile, c’est-à-dire que 99,5% des 8 954 mises à jour des votes sont moins coextrêmes que n’importe quel point de cette ligne. Comme nous pouvons le constater, les quatre mises à jour des votes en question (les deux points rouges, les points verts bien au-dessus de cette ligne et le point jaune le plus éloigné) sont bien au-dessus de cette ligne. En effet, le moins extrême de ces points, représenté par le point rouge inférieur qui se trouve au-dessus de la courbe du 99,5e percentile, est le 7e point le plus coextrême de l’ensemble des 8 954 mises à jour des votes, et représente le 99,92e percentile.
Cela soulève une question évidente : à quoi pourraient ressembler ces mises à jour de vote si elles étaient moins extrêmes ?
Graphiquement, cela impliquerait de les déplacer vers le bas (représentant une marge plus faible) et vers la gauche (représentant un ratio plus faible). En théorie, il suffirait de calculer la distance la plus courte par rapport à une courbe particulière de niveau de percentile et de choisir cette combinaison particulière (marge, ratio). Ce faisant, nous ignorerions toutefois un aspect crucial de la nature des données. En particulier, la diminution du ratio pour une marge donnée implique une augmentation du nombre total de votes dans la mise à jour. En particulier, étant donné l’échelle des anomalies ici, cela impliquerait un scénario dans lequel un grand nombre de votes – peut-être des centaines de milliers – pour les deux candidats ont été en quelque sorte retenus. Bien qu’il soit possible que ce soit le cas, il s’agirait presque certainement d’une erreur de saisie de données à l’échelle de centaines de milliers de votes qui a affecté les deux candidats de manière égale ou presque égale. Puisque la marge est la mesure qui compte pour le résultat, s’il y a eu un jeu déloyal, il est beaucoup plus probable que des voix soient soustraites à l’un des candidats tout en étant ajoutées à l’autre.
Puisque nous n’apportons aucune hypothèse a priori sur ce à quoi ces mises à jour devraient ressembler, il est intéressant de considérer ce à quoi elles ressembleraient si ces ratios sont exacts et s’ils représentaient simplement le 99e percentile de coextrémité. Graphiquement, cela revient à prendre les quatre points en question et à les “tirer” vers le bas jusqu’au milieu des trois lignes noires tracées. Si cela était fait, ces actualisations de vote auraient des marges incroyablement plus faibles, mais seraient tout de même plus coextrêmes que 99 % des 8 954 actualisations de vote étudiées. Nous n’avons aucune raison positive de croire que c’était précisément le cas. En effet, les données dont nous disposons ne nous permettent pas d’avancer des arguments en faveur d’un résultat particulier. Il est simplement utile de se demander à quoi ressembleraient les mises à jour présentant ces ratios si elles étaient plus coextrêmes que seulement 99 % des 8 954 mises à jour de votes étudiées, par opposition à 99,92 %.
Si ces résultats semblent irréalistes ou invraisemblables, c’est le résultat de l’étrangeté de ces mises à jour de votes par rapport au reste de la distribution.
Tout d’abord, considérons la mise à jour de l’IM à 6 h 31 HNE le 11/4. Son produit est de 77,3, et sa paire de coordonnées (marge, log-ratio) était (15,494, 4,989) [20]. S’il ne devait se trouver qu’au 99e percentile de coextrémité, alors son produit ne serait que de 6,600. Ainsi, si la valeur du log-ratio (normalisé) de 4,989 est maintenue constante, la valeur de la marge (normalisée) ne serait que de 1,323, au lieu de 15,494.
À ce stade, nous devons annuler le processus de normalisation qui nous permet de comparer équitablement les valeurs entre les États. Puisque ceux-ci ont été standardisés par rapport aux mises à jour des votes dans le Michigan, nous pouvons déterminer la valeur réelle de la marge correspondant à un z-score[21] de 1,323. En cherchant la marge numérique qui correspond dans le Michigan à un score Z de 1,323[22], nous voyons qu’elle est d’environ 11 834, alors que le score Z de cette observation réelle était de 15,494, correspondant à une marge de 135 424. En d’autres termes, si nous maintenons le ratio constant, et que cette mise à jour des votes ne se situait qu’au 99e percentile de coextrémité, la marge de cette mise à jour des votes aurait été de 123 590 voix de moins.
Considérons maintenant la mise à jour du WI à 3:42 AM CST le 11/4. Son produit est 46,452 et sa paire de coordonnées (marge, log-ratio) était (14,427, 3,220). S’il ne devait se trouver qu’au 99e percentile de coextrémité, alors son produit serait de 6,600. Ainsi, si la valeur du log-ratio (normalisé) de 3,220 est maintenue constante, la valeur de la marge (normalisée) ne serait que de 2,050, au lieu de 14,427. En recherchant la marge numérique qui correspond au Wisconsin à un score Z de 2,050 [23], nous voyons qu’elle est d’environ 16 938, alors que le score Z de cette observation réelle était de 14,427, ce qui correspond à une marge de 118 396. En d’autres termes, si nous maintenons le ratio constant, et que cette mise à jour du vote ne se situait qu’au 99e percentile de coextrémité, la marge de cette mise à jour du vote aurait été de 101 459 voix de moins.
Considérons maintenant la mise à jour de l’AG à 1:34AM EST le 11/4. Son produit est de 33,233 et sa paire de coordonnées (marge, log-ratio) était (12,836, 2,589). S’il ne devait se trouver qu’au 99e percentile de coextrémité, alors son produit serait de 6,600. Ainsi, si la valeur du log-ratio (normalisé) de 2,589 est maintenue constante, la valeur de la marge (normalisée) ne serait que de 2,549, au lieu de 12,836. En recherchant la marge numérique qui correspond en Géorgie à un score Z de 2,549 [24], nous voyons qu’elle est d’environ 21 250, alors que le score Z de cette observation réelle était de 12,836, ce qui correspond à une marge de 107 143. En d’autres termes, si nous maintenons le ratio constant, et que cette mise à jour du vote ne se situait qu’au 99e percentile de coextrémité, la marge de cette mise à jour du vote aurait été de 85 892 voix de moins [25].
Enfin, considérons la mise à jour du Michigan à 3 h 50 HNE le 11/4. Son produit est de 22,219 et sa paire de coordonnées (marge, log-ratio) était de (5,679, 3,912). Si elle ne devait être qu’au 99e percentile de coextrémité, alors son produit serait de 6,600. Ainsi, si la valeur du log-ratio (normalisé) de 3,912 est maintenue constante, la valeur de la marge (normalisée) ne serait que de 1,687, au lieu de 5,679. En recherchant la marge numérique qui correspond dans le Michigan à un z-score de 1,687 [26], nous voyons qu’elle est d’environ 15,009, alors que le score Z de cette observation réelle était de 5,679, ce qui correspond à une marge d’environ 49,8929. En d’autres termes, si nous maintenons le ratio constant, et que cette mise à jour du vote ne se situait qu’au 99e percentile de coextrémité, la marge de cette mise à jour du vote aurait été de 34 819 voix de moins [27].
En mettant tout cela en commun, nous constatons que si les quatre actualisations de vote étaient extrêmes – mais pas autant – la différence de marge serait supérieure à la marge de victoire dans les trois États.
À tout le moins, il est possible d’affirmer avec certitude que la victoire de Joe Biden dans ces trois États repose sur quatre des sept mises à jour de votes les plus coextrêmes de l’ensemble des 8 954 mises à jour de votes.
Considérations importantes
Il est important de noter un indicateur crucial de la raison pour laquelle ces résultats sont bizarres. Dans pratiquement tous les autres cas, les zones qui sont très pro-Biden ou pro-Trump ont des mises à jour de vote de taille variable, et donc une grande mise à jour de vote favorisant fortement un candidat est presque toujours accompagnée de mises à jour encore plus petites qui ont une plus grande variance dans le ratio, et au moins certaines d’entre elles favoriseront le candidat qui a gagné le plus grand lot.
En particulier, pour accepter comme légitimes les résultats observés dans le Michigan, il faudrait croire que la ou les deux zones de l’État les plus susceptibles d’être favorables à Biden ont en quelque sorte vu leurs bulletins de vote entièrement comptés en une ou deux mises à jour. Si les bulletins étaient comptés progressivement et publiés en plus petits lots, comme c’est généralement le cas, on s’attendrait à voir des mises à jour plus petites avec une plus grande variance dans les résultats, et on verrait presque certainement des mises à jour avec un ratio Biden:Trump plus élevé que les deux mises à jour du Michigan discutées dans ce rapport.
En effet, si l’on découvre par la suite qu’ils ne représentent pas la totalité du décompte (que ce soit pour les votes par correspondance ou pour l’ensemble des votes) dans ces zones, ces résultats doivent être considérés avec une extrême suspicion. Bien que le décompte des votes ne soit en aucun cas un échantillon aléatoire à l’échelle nationale, il finit par l’être si la sous-population dans laquelle les votes sont comptés est suffisamment petite. Si ceux qui ont accès aux séries chronologiques de données au niveau des comtés (ou des circonscriptions) peuvent démontrer que, pour les comtés ou les circonscriptions mentionnés dans cette mise à jour, il y a eu d’autres mises à jour (ou d’autres mises à jour avec des bulletins de vote par correspondance), alors ces résultats deviennent presque impossibles à croire. En d’autres termes, la crédibilité de ces mises à jour repose sur l’hypothèse que la ou les deux parties de l’État les plus favorables à Biden (peut-être par type de bulletin) ont été comptées entièrement dans ces deux lots. S’il n’est pas possible de démontrer que les bulletins comptés pendant ces pics étaient qualitativement différents de toutes les autres mises à jour des votes dans le Michigan, alors les résultats sont probablement trop extrêmes sur plusieurs plans pour être acceptés tels quels.
Il faudrait également croire que les votes par correspondance, qui sont généralement considérés comme étant plus favorables à Biden, parfois de manière substantielle, ont été comptés dans leur intégralité dans ces régions. Bien que cet ensemble de données ne fournisse pas de ventilation du nombre de votes dans chaque mise à jour provenant de différents types de votes, il est extrêmement surprenant que nous ne voyions pas de mises à jour de votes plus petites avec des votes par correspondance qui favorisent plus fortement Biden.
C’est également le cas dans le Wisconsin, où la mise à jour examinée dans ce rapport, qui présentait de loin la plus grande marge de Biden, présentait également le deuxième rapport Biden:Trump le plus élevé, de peu. Pour accepter ces résultats, il faut croire que le sous-ensemble de votes le plus favorable à Biden – par zone géographique et par type de vote – a été compté entièrement en un seul lot. Il serait extrêmement surprenant que tous les bulletins de vote par correspondance des deux comtés les plus favorables à Biden de l’État, les comtés de Dane et de Milwaukee, soient entièrement contenus dans ce lot, ce qui soulève la question de savoir pourquoi nous n’avons pas vu encore plus de mises à jour pro-Biden dans des mises à jour plus petites et à plus forte variance dans ces zones fortement démocrates. Si nous devons accepter que ces votes ont été comptés entièrement dans un seul lot, cela soulève également de sérieuses questions. En particulier, étant donné l’ambiguïté – à ce jour – quant à l’endroit où le processus de totalisation des votes a été arrêté et pourquoi, il n’est pas logique que ces votes aient été publiés en un lot aussi important.
Tout cela est particulièrement surprenant lorsqu’on le compare à l’analyse dominante de l’élection, à savoir que la victoire de Joe Biden est le résultat d’une meilleure performance dans les zones suburbaines. Si l’on regarde la carte des résultats finaux par comté, il est fort probable que ces mises à jour des votes proviennent des comtés urbains à plus forte densité de population où les ratios de Biden étaient beaucoup plus élevés. Les résultats obtenus ici remettent toutefois en question cette hypothèse, car nous pouvons constater qu’il s’est fortement appuyé sur quatre mises à jour de votes extrêmement aberrantes, qui se trouvaient presque certainement dans des zones urbaines fortement favorables à Biden, pour obtenir le coup de pouce dont il avait tant besoin aux premières heures du 4 novembre.
Conclusion
Ce rapport étudie 8 954 mises à jour individuelles des totaux des votes dans les 50 États et constate que quatre mises à jour individuelles – dont deux ont été largement remarquées sur Internet, y compris par le président – sont profondément anormales ; elles s’écartent d’un modèle que l’on retrouve par ailleurs dans la grande majorité des 8 950 mises à jour de votes restantes. Les conclusions présentées dans ce rapport [28] suggèrent que quatre mises à jour du décompte des voix – qui ont été collectivement décisives dans le Michigan, le Wisconsin et la Géorgie, et donc décisives pour un nombre critique de quarante-deux votes électoraux – sont particulièrement anormales et méritent une enquête plus approfondie.
En particulier, le fait de constater que les données plus larges suivent des schémas généraux et notre capacité à mesurer à quel point une mise à jour de vote individuelle suit – ou ne suit pas – ce schéma nous permet de faire des affirmations concrètes sur le caractère extrême d’une mise à jour de vote donnée et sur ce à quoi une mise à jour de vote particulière aurait pu ressembler si elle avait été moins extrême sur un axe ou un autre.
Nous constatons également que si ces mises à jour étaient seulement plus extrêmes que 99 % de toutes les mises à jour nationales en termes d’écart par rapport à ce modèle généralement observé, Joe Biden aurait très bien pu perdre les États du Michigan, du Wisconsin et de la Géorgie, toutes choses égales par ailleurs, et il aurait obtenu 42 voix électorales de moins, ce qui le placerait en dessous du nombre requis pour remporter la présidence. Quoi qu’il en soit, il est indiscutable que sa marge de victoire dans ces trois États repose sur les quatre mises à jour de votes les plus anormales identifiées par la métrique développée dans ce rapport.
Nous notons une fois de plus que cette analyse est largement limitée à quatre mises à jour de vote individuelles sur un échantillon de près de 9 000. Ce rapport ne suggère en aucun cas d’arrêter les enquêtes dans le Michigan, le Wisconsin, la Pennsylvanie, la Géorgie ou ailleurs ; c’est simplement que ces quatre mises à jour clés des bulletins de vote sont toutes profondément anormales par rapport à une métrique qui élimine toute composante de différents États ayant des penchants partisans différents ou un nombre différent d’électeurs. En outre, cette analyse n’exige pas que nous considérions les totaux finaux des votes dans l’un de ces États (ou comtés) comme suspects, ni, surtout, que nous acceptions que les données observées suivent une distribution particulière a priori. Nous montrons simplement que les données, ajustées de manière appropriée pour éliminer les différences de taille et de tendance politique entre les États, suivent un certain modèle, et que quatre mises à jour clés des votes s’écartent profondément de ce modèle.
Nous pensons que la nature extraordinairement anormale des mises à jour du vote étudié ici, combinée aux implications politiques stupéfiantes, exige une enquête immédiate et approfondie.
Correction : dans une version précédente de cet article, la probabilité que les mises à jour des votes en Géorgie, au Wisconsin et au Michigan constituent cinq des dix mises à jour les plus extrêmes était de 0,0037 %. La valeur réelle est plus proche de 0,99 %. Les auteurs s’excusent pour cette erreur et l’article a été corrigé en conséquence.
